感染症の蔓延をどうとらえるべきか？：「感染症数理疫学」をちょっとかじってみて 新型コロナのアカデミックなアプローチ

杉林　堅次

１．はじめに

　昨年4月からいろんな先生方に書き継いでいただいた本学のHP中に掲載している「新型コロナウイルス感染症（COVID-19）関連の特集記事（コラム）シリーズ」に再度原稿を提出するにあたって、前書きに２つのキーワードを用意しました。
　キーワードの１つ目は物語「復活の日」です。この物語は小松左京氏が1964年に書き起こしたもので、この原作に従った映画が（旧）角川春樹事務所とTBSの製作により1980年に東宝系で公開されました。先日、この映画を40年ぶりに見ました。ちなみに英題は「Virus」です。生物兵器として開発中であったウイルスMM-88がスパイによって持ち去られるところから物語は始まります。しかし、スパイの乗った小型飛行機が吹雪に遭って山中に墜落し、保管容器からウイルスが拡散して世界中にウイルス肺炎感染症を引き起こすことになります。ウイルス肺炎感染症なんてCOVID-19と同じです。ちなみに、パンデミックは人間の心にも感染し、この物語では核弾頭を掲載したミサイルが発射され、世界は2度死ぬことになります。40年前に見た時は核の恐怖が高かった時代でしたので核の物語に注目してしまい、ウイルスの話にはちょっと現実感をもてなかったことを思い出します。この映画を再度みたのは、もちろんタイトルが「Virus」であることと、いまその先見性が見直されている小松氏の全集がなんと「城西国際大学出版会」から出されていることが理由でした。皆さんもオンライン授業の空き時間にでも、「復活の日」の映画をみるか小説を読んでみてください。
　前述した本学HPのCOVID-19関連のコラム特集の最初の記事を4月3日に書かせていただきました。この時は、4月2日に予定されていた入学式がいつも通りできなかったので、少しでも明るいニュースをと思い、また、いずれはCOVID-19 も克服されることを伝えたくて、COVID-19治療薬の開発現状について解説しました。昨年暮れごろからワクチン開発のニュースが増えてきました。我が国でも2月末から接種が始まると報道されていますね。
　もう1つのキーワードには、今回のコロナ禍が始まってすぐに調べた「スペイン風邪」を選びました。「スペイン風邪」は、1918年1月から1920年12月までに世界中で5億人もの人が感染したパンデミックです。これは当時の世界人口20億人の約4分の1にも相当します。死者数は1,700万人から5,000万人との推計が多いですが、1億人に達した可能性も指摘されています。まさに、人類史上最悪の感染症の1つです。当時はまだ電子顕微鏡がなく、ウイルスという存在は知られていませんでした（ちなみにウイルスが原因の黄熱病で倒れた野口英世の没年は1928年です。野口英世びいきかもしれませんが、あの時代に電子顕微鏡があれば、ウイルスは研究熱心な彼によって発見されたのではないかと思っています）。なお、近年の研究により、「スペイン風邪」はA型インフルエンザウイルスの亜型の一つであるH1N1によるものと判明しています。H1N1によるパンデミックは、「スペイン風邪」と11年前の2009年の新型インフルエンザの2回であると言われています。皆さんはH1N1のサバイバーですね。さて、私が言いたいのは、「スペイン風邪」から約100年を経過して、我々人類はあの経験をいま生かせているのかということです。「東日本大震災」についても同様なことが言われていますが、我々はCOVID-19に関する経験も語り継がねばなりません。特に、若くしてこの苦難を経験している学生の皆さんには、これからの対応も含め、「語り部」として引き継いでいただきたいと願っています。

２．感染症数理疫学と薬物動態学

　年が明けて、1月8日に2月7日までの緊急事態宣言が発出されました。COVID-19の終息はいつ迎えるのか。人と人との距離（physical distance）を考えて行動するのはいつまでなのか。皆さんも心配でしょう。昨年4月7日最初の緊急事態宣言が出された頃、突如、北海道大学の西浦博先生（現、京都大学）のお名前をテレビや新聞で目にするようになりました。彼はCOVID-19の蔓延の度合いは「感染症数理疫学」で解けると説明されました。そんなに簡単でないと揶揄する方も現れたようですが、私はどのようにして感染症数推移モデルをたて計算式にしていくのかと関心を持ちました。私の専門の１つに「薬物動態学」があります。「薬物動態学」は薬を投与されたヒトの体内において薬の量または濃度が経時的にどのように変動していくかを評価する学問です。一方、「感染症数理疫学」はある地域にバクテリアやウイルスに感染した人の数が経時的にどのように変動していくかを評価する学問ということです。お互いに似ていると感じました。そこで、もちろん私の専門外ではありますが、「感染症数理疫学」の初歩を勉強して昨年半ばに仲間とともに学会誌に投稿し、暮れに掲載されました¹⁾。皆さんにもウイルス感染者数推移の考え方の一部を披露したいと思います。

３．SIR モデル

　SIR モデルについて説明します。感染可能人数（susceptibles：感染する可能性のある人数）、感染者数（infectives：感染し、かつ感染させる能力のある人数）、病気から快復した人数 （recovered/removed：病気から快復した免疫保持者、ただし、死亡者含む）をそれぞれS(t)、I(t)、R(t)とします（(t)がついているのはS、I、Rそれぞれが時間の関数であることを意味します）。このときケルマックとマッケンドリックの提起したモデル²⁾では、その最も単純な感染ケースは、S、I、Rの3つのコンパートメントを繋ぐ以下のような常微分方程式によって表されると言われています。

dS(t)/dt = -βS(t)I(t)
dI(t)/dt = βS(t)I(t)γI(t)    (1)
dR(t)/dt = γI(t)  

ここでβは感染率、γは快復率（隔離率）を表します。感染率βは、（1 回の接触で感染する比率）×（単位時間に接触する回数）で示されます。たとえば、単位時間を１日とすると、1 回の接触で0.000005（5×10^-6）の比率で感染し、１日に10 回接触したとすると感染率βは0.00005（5×10^-5）となります。一方、快復率γは一か月（30日）で緩解とするなら、1/30で0.033となります。また、βI(t) は感染力（force of infection）を示し、時間tにおける単位時間あたり単位人数あたりの感染率を表します。一般にこのように人数を病気の状態に従って3つのコンパートメントで示した感染症モデルをSIR モデルといいます²⁾。感染しても感染性のない状態（latent period/exposed class）や感染後症状の発症しない状態（潜伏期間：incubation period）などを考慮する場合には、感染状態はさらに分割されて、４つのコンパートメントからなるモデル（SEIRモデル）を用いるようです。また、免疫性の獲得が恒久的なものでなければR → Sという状態変化が可能となり、そうした場合はSIRSモデルなどが用いられるということです。数学や統計学に関心のある方は、インターネットで「感染症数理疫学」や「SIR モデル」と入力すれば学ぶ材料に事欠きません（学生時代に薬の生体組織への広がりを表す拡散方程式（偏微分方程式です）を解きなさいと課題が出ました。指導教官もよくわからないと言います。しかたなく図書館や本屋をめぐりました。結局、拡散方程式と似ている熱伝導の数式にぶち当たり、解くことができました。今はインターネットがあるのでいろいろ探し回らずとも必要な文献や資料がすぐに手に入ります。学ぶのには大変良い時代になりました）。

４．SIRモデルを解く

　式(1)からはおそらく厳密解は求まりません。そこで、私は式(1)をまず差分方程式で解こうと考えました。式(1)を差分方程式で表記すれば以下のようになります。

（Si+1-Si）/（ti+1-ti）= -βSiIi
（Ii+1-Ii）/（ti+1-ti）= βSiIi-γIi　　(2)
（Ri+1-Ri）/（ti+1-ti）= γIi

これらの式は、以下のようになります。

Si+1= Si｛1－βIi（ti+1– ti）｝
Ii+1= Ii｛1＋（βSi− γ)(ti+1– ti）｝   (3)
Ri+1= Ri＋γIi（ti+1– ti）

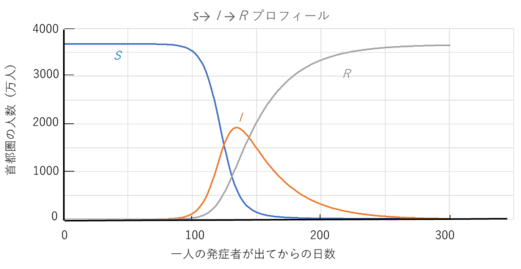
　次に式(3)をエクセル中で「あてはめ計算」することにしました。エクセルの一番左のカラム（列）にt_iを、次にS_i、そしてI_i、さらにはR_iとして、また、iを０行からn行としました。ここで、t_i+1-t_i、β、さらにはR_iに種々数字を入力してシミュレーションしてみることにしました。また、人の数は首都圏の人口（東京都、埼玉県、千葉県、神奈川県の和、3,676万人）としました。t_i+1-t_i=1、β = 0.00005、さらにはγ = 0.033としたときの結果を図1に示します。時間0に1名の感染者が出たと考えています。もちろん、入力したパラメータが適切とはいえないですが、この図ではなんと半数の人々が感染することになります。また、注意して見ていただきたいのは、半数が感染するとしても3か月間も潜在期間（感染者がほとんど出ない期間）があることです。西浦先生は人と会う回数を減らすとよいと言われました。人と会う回数を減らすと、すなわちβを減らすと、感染人数は少なくなるのは当然ですが、興味深いのは感染時期が遅れるということです（パラメータをいろいろ変えてみても潜在期間はかなり長いです）。もちろん、感染時期が遅れれば医療の対策などを行う時間の余裕ができます。

図1  感染可能人数、感染者数、病気から快復した人数の経時変化の例

　このエクセルで解析するとき、時々計算値が出ないときがありました。城西大学の数学科の先生に図々しくもお聞きしました。先生からは4次のルンゲ・クッタ法で解けば、解が発散したり不正確になったりはしないと言っていただきました。私は学生時代に自分でルンゲ・クッタ法にチャレンジしたことがありましたがすっかり忘れていましたので、また、インターネットを使って探してみました。その結果、「数値計算を使って常微分方程式を解く：ルンゲ・クッタ法の解説」⁴⁾や「SIRモデル（コロナウイルス感染の微分方程式）」というサイト⁵⁾が出てきました。前者はこの分野を始める方に有用なサイトだと思います。また、後者は数値を入れると簡単にシミュレーション値が出てくるので、数学や統計学が苦手な方でも使えると思います。ただし、これらの詳細な説明は、専門的になりすぎるのでここでは割愛させていただきます。ちなみに、βS(0)/γ>1のとき、流行初期の段階で感染は拡大し、感染者数は指数関数的に増加します。また、βS(0)/γ<1ならば、感染の流行は発生せず、感染者数は自然に減衰していきます。さらに、γ=0なら当然全ての人が感染します。このとき感染者数Iはロジスティック関数になり、感染者数-時間の関係がシグモイド型になります。 そろそろ頭が痛くなってきた方も多いと思います。頭痛がしない方は「感染症の流行モデル SIRモデル」⁶⁾を参照してください。

５．終わりに

　今回のコロナ禍を経験して、厚生労働省が公的病院の再編統合を検討していましたが、実際に再編統合される前で本当に良かったと思っています。医療の逼迫を少しでも遅らせているのではないかと思います。一方で、地方の保健所の多くはすでに整理されていました。保健所の職員の忙しさが報道されていますが、保健所の統合などの決定はちょっと勇み足ではなかったかと思いました。たしかに、我が国は少子高齢化度で世界でのトップランナーになっており、医療費の増大が全体の経済を押し下げていることも事実です。しかし、医療の質の向上は医療者の技能や最新の医療機器の充実度だけでなく、新規感染症の蔓延のように予想できないようなことにも対応できる余裕だと思います。本学では看護師、薬剤師、理学療法士、社会福祉士、介護福祉士などの医療職・福祉職を輩出しています。医療職・福祉職に就いた卒業生が新規感染症などの蔓延時にも心おきなく活躍できる社会となることを願っています。
　最近は「スペイン風邪」だけでなくSARS（重症急性呼吸器症候群、2002から03年）やMERS（中東呼吸器症候群、2012年から現在）の話も出てきます。SARSは日本にはほとんど被害がありませんでしたが、中国（香港、台湾を含む）に蔓延しました。MERSは中東地域をはじめ中国や韓国にも広がりました。韓国はこの時の状況をしっかり観察しPCRの検査システムを充実したと聞きます。中国もこの時の反省がしっかりあるのではないかと思います。しかし、日本はお隣の中国や韓国の状況についても表面しか観察せず、他国の医療システムの変遷について考察することがなかったのかと思います。本学は国際大学です。しっかりした国際連携があれば、こういう失敗も少なくなっていくかと期待します。国連の提唱している持続可能な開発目標（SDGs）も一つの国では達成できません。本学のような国際大学がSDGsの達成にももっと寄与できるのではないかと考えています。私達が気を引き締めることはもちろんですが、本学の学生や本学で学ぶ留学生の将来の活躍にも期待したいと思います。
　今回私がトライしたように、皆さんも専門外の領域を勉強するのも良いかと思います。いまは、インターネットを使えば適切なサイトが見つかります。また、大学は教員の宝庫です。どこかに専門の方がおられます。いまは、オンライン授業や対面授業とのハイブリッド授業が定着してきて、対面の授業だけより質問しやすく教員とも距離が縮まったと評価されています。このコロナ禍の状況を忘れないためにも、皆さんも専門外の事柄にチャレンジしてくれるとうれしいです。

謝辞
SIRモデルの解法にご示唆を頂いた城西大学数学科の先生に感謝します。  

参考文献

1. 杉林 堅次、森 健二、押坂 勇志、武井 千弥、藤堂 浩明、板倉 祥子、高山 幸三、感染から治癒過程を表現する「感染症数理疫学」と吸収から消失過程を表現する「薬物動態学」の類似点と相違点(2020),薬剤学,80(6),322-329
2. W.O. Kermak, R.M. MacKendrick (2000), Virus dynamics: Mathematical Principles of Immunology and Virology, Oxford University Press, Oxford.
3. 西浦博、稲葉寿、感染症流行の予測：感染症数理モデルにおける定量的課題(2006), 統計数理, 54, 461-480.
4. http://shimaphoto03.com/science/rk-method/
5. https://keisan.casio.jp/exec/user/1585989999
6. https://nekodamashi-math.blog.ss-blog.jp/2020-03-03